Modelado numérico: qué es, métodos y cálculo aplicado con Ansys
El modelado numérico es la técnica que permite representar y analizar fenómenos físicos o sistemas complejos mediante ecuaciones matemáticas resueltas con ayuda de ordenadores. Se fundamenta en el uso de métodos numéricos y en el cálculo numérico, disciplinas que hacen posible obtener soluciones aproximadas a problemas que no pueden resolverse de forma analítica. Gracias a esta metodología, ingenieros y científicos pueden simular el comportamiento de estructuras, fluidos, materiales o campos electromagnéticos antes de construir prototipos o realizar ensayos reales, reduciendo costes y aumentando la fiabilidad de los diseños.
Fundamentos del modelado numérico
El modelado numérico se apoya en tres pilares:
- Formulación matemática: se expresan las leyes físicas mediante ecuaciones diferenciales.
- Métodos numéricos: algoritmos que permiten discretizar y resolver esas ecuaciones.
- Cálculo numérico: estudio de la precisión, estabilidad y eficiencia de los algoritmos empleados.
La combinación de estos elementos convierte al modelado numérico en una herramienta esencial para validar teorías y optimizar procesos industriales.
Métodos numéricos más utilizados
Los principales métodos numéricos aplicados en modelado son:
Método de los elementos finitos (MEF):
Divide una estructura en pequeñas partes llamadas elementos, permitiendo calcular tensiones, deformaciones y vibraciones.
Método de volúmenes finitos (MVF):
Se emplea en dinámica de fluidos para simular turbulencia, transferencia de calor y procesos de combustión.
Método de diferencias finitas:
Aproxima derivadas mediante discretización en mallas regulares, útil en problemas de difusión y ondas.
Cada método tiene ventajas y limitaciones, y la elección depende del fenómeno a estudiar y de los recursos computacionales disponibles.
Ansys como plataforma de modelado numérico
El software ANSYS es uno de los líderes mundiales en simulación y análisis numérico. Su éxito radica en que integra distintos métodos numéricos en un entorno unificado:
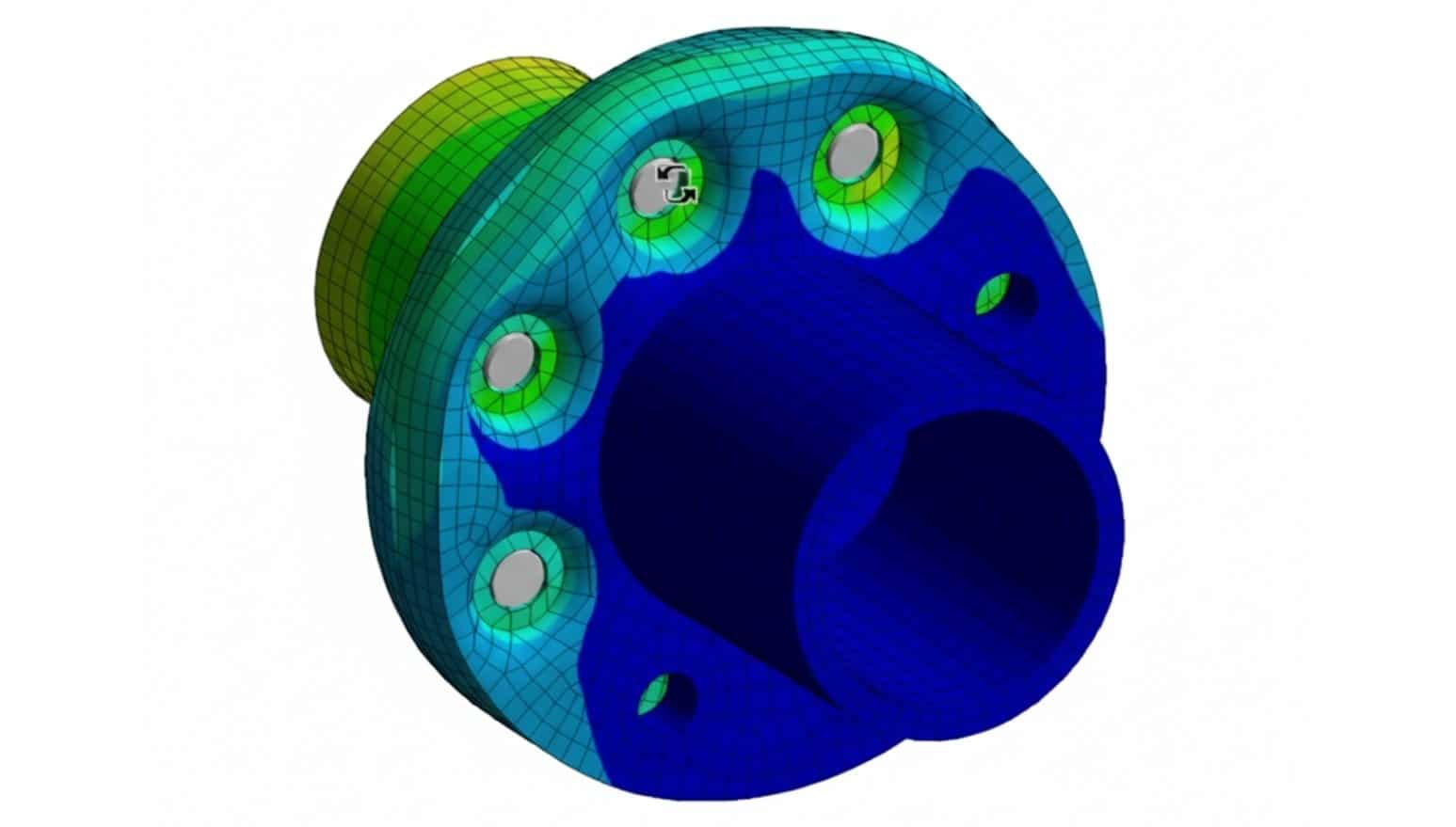
- Ansys Mechanical: aplica el MEF para análisis estructural avanzado.
- Ansys Fluent: utiliza MVF para simulaciones de fluidos y transferencia térmica.
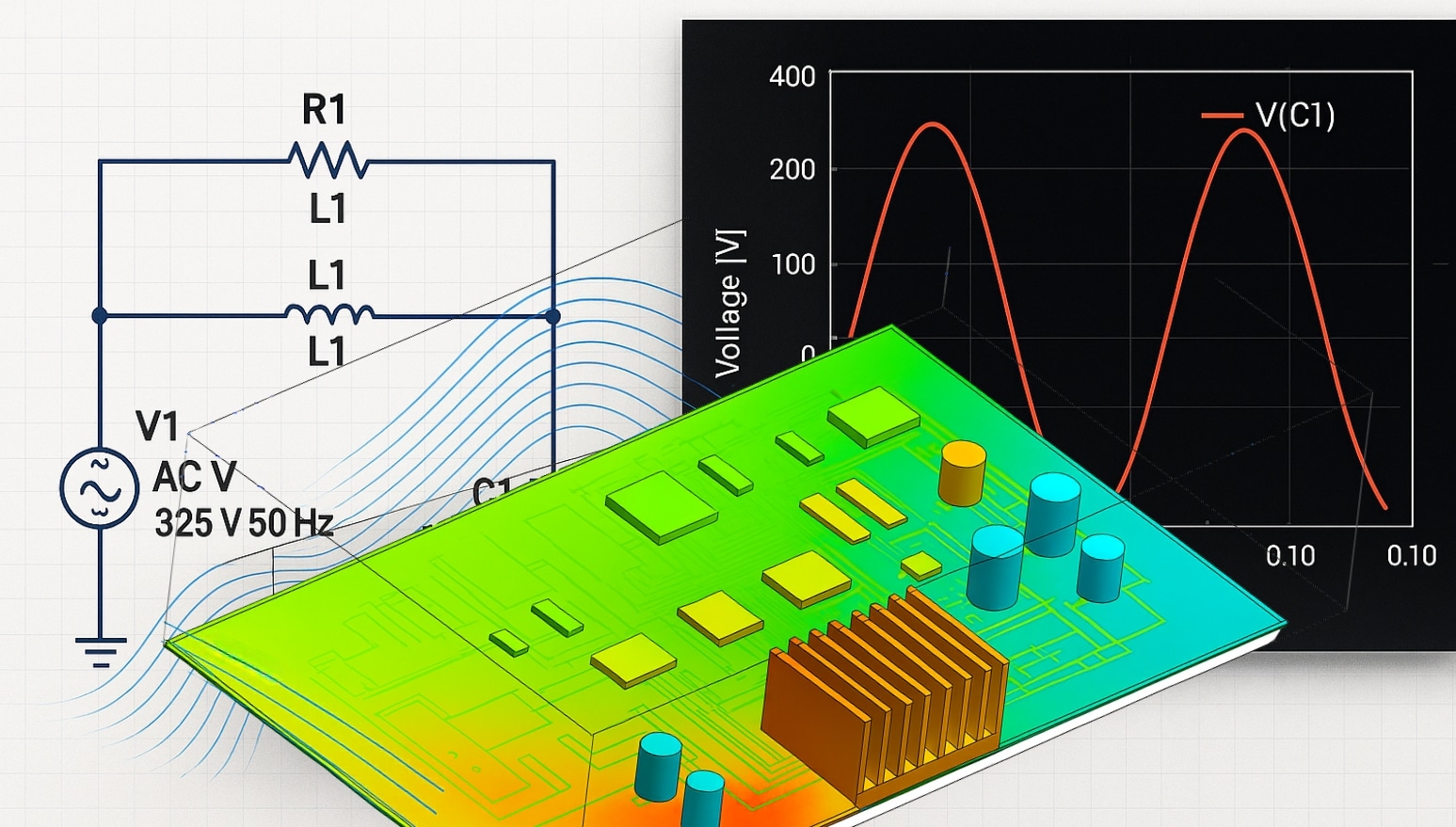
- Ansys Maxwell: especializado en electromagnetismo y diseño de dispositivos eléctricos.
- Ansys Discovery: permite exploraciones rápidas de diseño con simulaciones inmediatas.
ANSYS convierte el cálculo numérico en resultados prácticos, ofreciendo precisión y versatilidad para ingenieros de múltiples disciplinas.
Aplicaciones del modelado numérico con Ansys
El modelado numérico tiene un impacto transversal en la ingeniería moderna:
- Mecánica estructural: cálculo de tensiones y deformaciones en piezas y estructuras.
- Aeroespacial: simulación aerodinámica y resistencia de materiales.
- Energía: optimización de turbinas, sistemas eléctricos y procesos térmicos.
- Construcción civil: diseño de cimentaciones, túneles y puentes con seguridad reforzada.
- Electrónica: análisis de campos electromagnéticos y diseño de dispositivos.
Ventajas del modelado numérico con Ansys
- Precisión: resultados fiables gracias a algoritmos validados de cálculo numérico.
- Ahorro de costes: reducción de prototipos físicos y ensayos experimentales.
- Seguridad: detección de fallos potenciales antes de la fabricación.
- Innovación: exploración de diseños disruptivos sin riesgo.
El modelado numérico es la base de la ingeniería moderna. Los métodos numéricos y el cálculo numérico proporcionan el marco teórico, mientras que ANSYS convierte esa teoría en simulaciones prácticas y aplicables.
Para ingenieros, investigadores y empresas, dominar el modelado numérico con ANSYS significa estar preparados para los retos tecnológicos del futuro, con soluciones más seguras, eficientes e innovadoras.
You May Also Like
Ansys Ensight: postprocesado avanzado para ingeniería CAE
Ansys Ensight es una herramienta de postprocesado avanzada para analizar y visualizar resultados de
Simulación de circuitos eléctricos con ANSYS: precisión, multiphysics y validación avanzada para ingeniería moderna
La simulación de circuitos eléctricos con ANSYS permite validar sistemas complejos con precisión
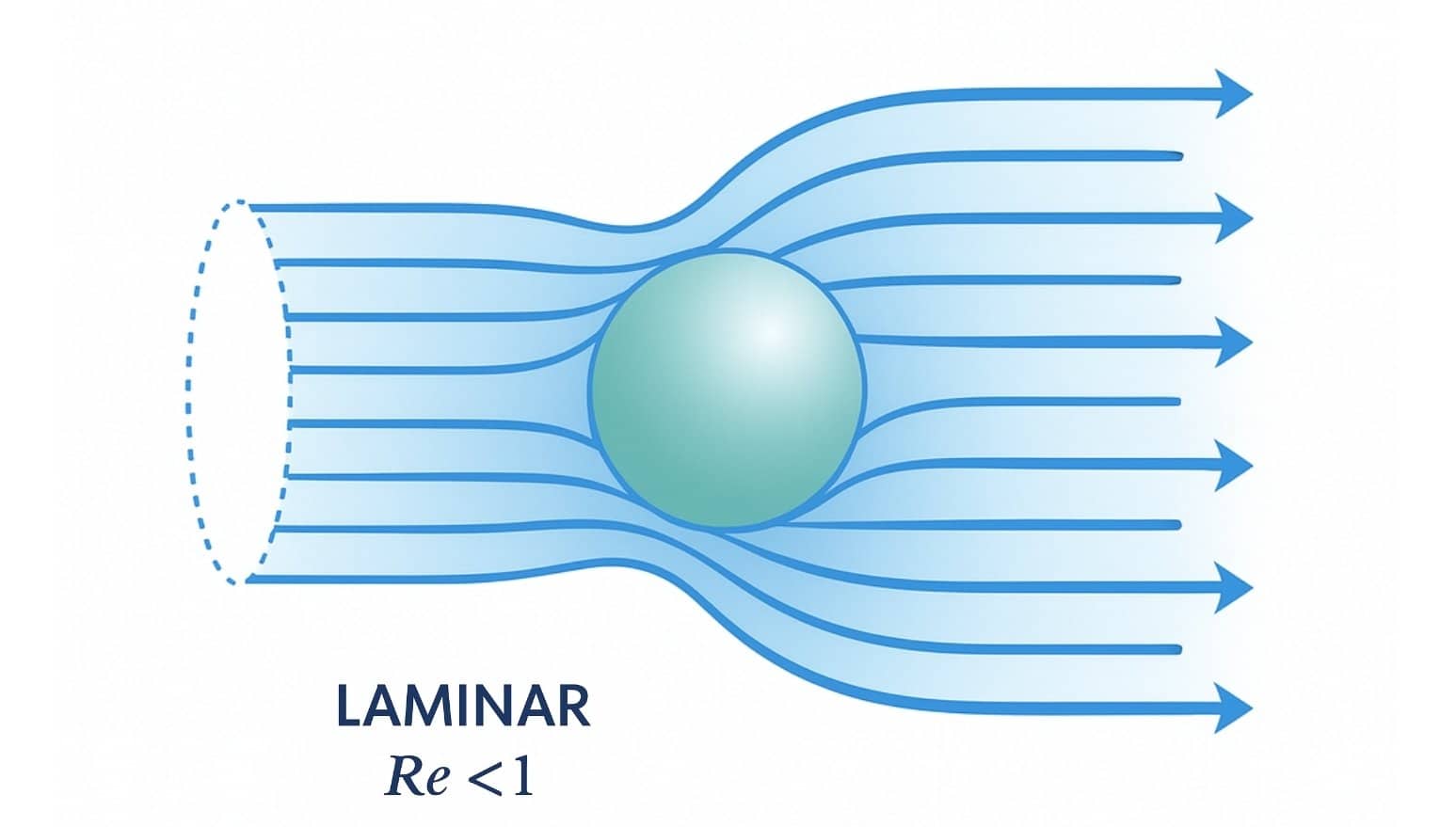
Flujo laminar: qué es y cómo predecirlo mediante simulación avanzada con Ansys
El flujo laminar es un movimiento del fluido en capas estables y previsibles, cuya simulación con A